100+ bài tập toán lớp 9 Đại số, Hình học (Có kèm đáp án)

Nếu bạn muốn giúp các bé tăng khả năng rèn luyện môn Toán và có thể đạt điểm cao trong các kì thi thì có thể tham khảo những bài tập toán lớp 9 sau đây. Những tài liệu chất lượng này sẽ đảm bảo các em ôn luyện đạt hiệu quả. Nhằm giúp các bậc phụ huynh, seolalen.vn đã sưu tầm và tổng hợp hơn 100 bài tập toán lớp 9 có chọn lọc kèm đáp án. Bạn có thể tham khảo ngay sau đây.

Xem thêm: [Tổng hợp] 50+ bài tập toán lớp 2 từ cơ bản đến nâng cao 2022

80 BÀI TẬP TOÁN LỚP 9 VỀ HÌNH HỌC (CÓ KÈM ĐÁP ÁN)

80 bài tập toán lớp 9 về hình học có kèm đáp án này sẽ giúp các em học sinh ôn tập, rèn luyện kỹ năng, kiến thức từ đó có thể đạt kết quả cao trong các bài kiểm tra hay kỳ thi.

>> Link tải tài liệu hình học toán lớp 9: TẠI ĐÂY

Bài 1. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao AD, BE, CF cắt nhau tại H và cắt đường tròn (O) lần lượt tại M,N,P.

Chứng minh rằng:

1. Tứ giác CEHD, nội tiếp .
2. Bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. AE.AC = AH.AD; AD.BC = BE.AC.
4. H và M đối xứng nhau qua BC.
5. Xác định tâm đường tròn nội tiếp tam giác DEF.

Lời giải:

1. Xét tứ giác CEHD ta có:

Góc CEH = 90* (Vì BE là đường cao)

Góc CDH = 90* (Vì AD là đường cao)

=> góc CEH + góc CDH = 180*

Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp

2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEC = 90*.

CF là đường cao => CF ┴ AB => góc BFC = 90*.

Như vậy E và F cùng nhìn BC dưới một góc 90* => E và F cùng nằm trên đường tròn đường kính BC.

Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.

3. Xét hai tam giác AEH và ADC ta có: góc AEH = góc ADC = 90*; góc A là góc chung

=> Δ AEH ˜ Δ ADC => AE/AD = AH/AC=> AE.AC = AH.AD.

* Xét hai tam giác BEC và ADC ta có: góc BEC = góc ADC = 90*; góc C là góc chung

=> Δ BEC ˜ Δ ADC => AE/AD = BC/AC => AD.BC = BE.AC.

4. Ta có góc C1 = góc A1 (vì cùng phụ với góc ABC)

góc C2 = góc A1 ( vì là hai góc nội tiếp cùng chắn cung BM)

=> góc C1 = góc C2 => CB là tia phân giác của góc HCM; lại có CB ┴ HM => Δ CHM cân tại C

=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.

5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn

=> góc C1 = góc E1 (vì là hai góc nội tiếp cùng chắn cung BF)

Cũng theo chứng minh trên CEHD là tứ giác nội tiếp

góc C1 = góc E2 (vì là hai góc nội tiếp cùng chắn cung HD)

góc E1 = góc E2 => EB là tia phân giác của góc FED.

Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.

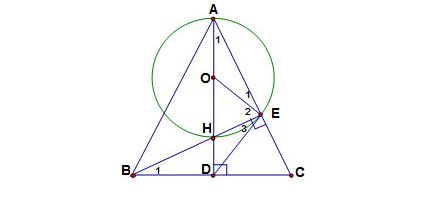
Bài 2. Cho tam giác cân ABC (AB = AC), các đường cao AD, BE, cắt nhau tại H. Gọi O là tâm đường tròn ngoại tiếp tam giác AHE.

Chứng minh tứ giác CEHD nội tiếp .

Bốn điểm A, E, D, B cùng nằm trên một đường tròn.

Chứng minh ED = 1/2BC.

Chứng minh DE là tiếp tuyến của đường tròn (O).

Tính độ dài DE biết DH = 2 Cm, AH = 6 Cm.

Lời giải:

1. Xét tứ giác CEHD ta có:

góc CEH = 90* (Vì BE là đường cao)

góc CDH = 90* (Vì AD là đường cao)

=> góc CEH + góc CDH = 1800

Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp

2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 90*.

AD là đường cao => AD ┴ BC => BDA = 90*.

Như vậy E và D cùng nhìn AB dưới một góc 90* => E và D cùng nằm trên đường tròn đường kính AB.

Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.

3. Theo giả thiết tam giác ABC cân tại A có AD là đường cao nên cũng là đường trung tuyến

=> D là trung điểm của BC. Theo trên ta có góc BEC = 90*.

Vậy tam giác BEC vuông tại E có ED là trung tuyến => DE = 1/2 BC.

4. Vì O là tâm đường tròn ngoại tiếp tam giác AHE nên O là trung điểm của AH => OA = OE => tam giác AOE cân tại O => góc E1 = góc A1 (1).

Theo trên DE = 1/2 BC => tam giác DBE cân tại D => góc E3 = góc B1 (2)

Mà góc B1 = góc A1 (vì cùng phụ với góc ACB) => góc E1 = góc E3 => góc E1 + góc E2 = góc E2 + góc E3

Mà góc E1 + góc E2 = góc BEA = 900 => góc E2 + góc E3 = 900 = góc OED => DE ┴ OE tại E.

Vậy DE là tiếp tuyến của đường tròn (O) tại E.

5. Theo giả thiết AH = 6 Cm => OH = OE = 3 cm.; DH = 2 Cm => OD = 5 cm. Áp dụng định lý Pitago cho tam giác OED vuông tại E ta có ED^2 = OD^2 – OE^2 ↔ ED^2 = 5^2 – 3^2 ↔ ED = 4cm

Bài 3: Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax , By lần lượt ở C và D. Các đường thẳng AD và BC cắt nhau tại N.

1. Chứng minh AC + BD = CD.
2. Chứng minh góc COD = 90*
3. Chứng minh AC.BD = (AB^2)/4
4. Chứng minh OC // BM
5. Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.
6. Chứng minh MN ┴ AB

Bài 4: Cho tam giác cân ABC (AB = AC), I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp góc A , O là trung điểm của IK.

1. Chứng minh B, C, I, K cùng nằm trên một đường tròn.
2. Chứng minh AC là tiếp tuyến của đường tròn (O).
3. Tính bán kính đường tròn (O) Biết AB = AC = 20 Cm, BC = 24 Cm.

Bài 5: Cho đường tròn (O; R), từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điểm M bất kì ( M khác A) kẻ cát tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). Kẻ AC ┴ MB, BD ┴ MA, gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB.

1. Chứng minh tứ giác AMBO nội tiếp.
2. Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn .
3. Chứng minh OI.OM = R^2; OI. IM = IA^2.
4. Chứng minh OAHB là hình thoi.
5. Chứng minh ba điểm O, H, M thẳng hàng.
6. Tìm quỹ tích của điểm H khi M di chuyển trên đường thẳng d

Bài 7: Cho đường tròn (O; R) đường kính AB. Kẻ tiếp tuyến Ax và lấy trên tiếp tuyến đó một điểm P sao cho AP > R, từ P kẻ tiếp tuyến tiếp xúc với (O) tại M.1. Chứng minh rằng tứ giác APMO nội tiếp được một đường tròn.

2. Chứng minh BM // OP.
3. Đường thẳng vuông góc với AB ở O cắt tia BM tại N. Chứng minh tứ giác OBNP là hình bình hành.
4. Biết AN cắt OP tại K, PM cắt ON tại I; PN và OM kéo dài cắt nhau tại J. Chứng minh I, J, K thẳng hàng.

Bài 8 Cho nửa đường tròn tâm O đường kính AB và điểm M bất kì trên nửa đường tròn (M khác A,B). Trên nửa mặt phẳng bờ AB chứa nửa đường tròn kẻ tiếp tuyến Ax. Tia BM cắt Ax tại I; tia phân giác của góc IAM cắt nửa đường tròn tại E; cắt tia BM tại F tia BE cắt Ax tại H, cắt AM tại K.

1) Chứng minh rằng: EFMK là tứ giác nội tiếp.

2) Chứng minh rằng: AI2 = IM . IB.

3) Chứng minh BAF là tam giác cân.

4) Chứng minh rằng : Tứ giác AKFH là hình thoi.

5) Xác định vị trí M để tứ giác AKFI nội tiếp được một đường tròn.

Bài 9 Cho nửa đường tròn (O; R) đường kính AB. Kẻ tiếp tuyến Bx và lấy hai điểm C và D thuộc nửa đường tròn. Các tia AC và AD cắt Bx lần lượt ở E, F (F ở giữa B và E).

1. Chứng minh AC. AE không đổi.
2. Chứng minh góc ABD = góc DFB.
3. Chứng minh rằng CEFD là tứ giác nội tiếp.

TỔNG HỢP CÁC DẠNG BÀI TẬP TOÁN LỚP 9 VỀ ĐẠI SỐ

Tài liệu bao gồm cả lý thuyết và bài tập về các nội dung: căn bậc 2 – căn bậc 3, mối liên hệ giữa phép nhân và khai phương, phép chia, biến đổi biểu thức chứa căn bậc 2 đơn giản, rút gọn biểu thức chứa căn bậc 2.

>> Link tải tài liệu đại số toán lớp 9: TẠI ĐÂY

Nội dung chính của tài liệu đại số bao gồm:

Chương I. Căn bậc hai – Căn bậc ba

1. Căn bậc hai số học
2. Căn thức bậc hai

Dạng 1: Tìm điều kiện để căn bậc 2 {A} có nghĩa

Dạng 2: Tìm giá trị biểu thức

Dạng 3: So sánh căn bậc 2

Dạng 4: Rút gọn biểu thức

Hy vọng những bài tập toán lớp 9 mà seolalen.vn mang đến đã giúp các em học sinh có đủ tài liệu để luyện tập, ôn thi trong mùa dịch này thật tốt. Nếu muốn tìm thêm nhiều tài liệu học tập khác cho các bé, bạn có thể liên hệ ngay seolalen.vn để được giúp đỡ nhé.