Tuyển chọn các đề thi giữa kỳ 1 toán 9 có đáp án được chọn lọc bởi các giáo viên giàu kinh nghiệm biên soạn và sưu tầm từ bộ đề từng các trường THCS hàng đầu. Hy vọng thông qua bộ đề thi sẽ giúp các em học sinh ôn tập, củng cố kiến thức tốt, nhanh chóng, đạt được kết quả tốt nhất.
Link tổng hợp đề thi giữa 1 Toán 9 – 10 đề
Tổng hợp 10 đề thi giữa kỳ 1 Toán 9 có đáp án đầy đủ và chi tiết nhất. Link tải TẠI ĐÂY
Tổng hợp các đề thi giữa 1 Toán 9 mẫu
Đề số 1
Đề thi Giữa Học kì 1
Năm học 2021 – 2022
Bài thi môn: Toán lớp 9
Thời gian làm bài:60 phút
(không kể thời gian phát đề)
(Đề số 1)
1. Giá trị lớn nhất của biểu thức bằng:
A. 2020 B. 2019
C. 2018 D.– 2019
2. Với x, y là số đo các góc nhọn. Chọn nội dung sai trong các câu sau:
3. Cho ΔABC vuông tại A ,đường cao AH, ta có:
4. Giá trị của biểu thức bằng:
A. -11 B. 121 C. -121 D. 11
5. Căn bậc hai số học của 4 là
A. 2 B. 8 C. 16 D. 4
6. Chọn khẳng định đúng:
A. cot720 = cot180 B. cos250= sin650
C. sin670= sin230 D. tan310 = cot310
7. Trong một tam giác vuông. Biết . Tính sinx.
8. Điều kiện để có nghĩa là:
9. Trục căn thức ở mẫu ta được:
10. Cho tam giác DEG vuông tại E, cosG bằng:
11. Căn bậc ba của -27 là:
A.9 B.3 C.-3 D.-9
12. Nếu sin α = thì cot α bằng:
13. Cho bằng:
14. Nếu cos x = sin 350 thì x bằng:
A.350 B.450 C.650 D.550
15. Tìm điều kiện để có nghĩa, ta có:
16. Tìm điều kiện để 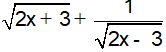
17. Biểu thức liên hợp của biểu thức là:
18. Căn bậc hai của 16 là:
A. -4 và 4 B. 16 C. -16 và 16 D. 4
19. Rút gọn biểu thức bằng:
A. 10 B. √40 C. 4√36 D. 40
20. Nếu α = 25018‘ thì cot α khoảng:
A. 0,47 B. 0,43 C. 0,9 D. 2,12
21. Cho tam giác ABC vuông ở A, BC = 25; AC = 20, số đo của góc C bằng:
A. 530 B. 370 C. 360 D. 540
22. Cho tam giác BDC vuông tại D, sinC bằng:
23. Các tia nắng mặt trời tạo với mặt đất một góc bằng 400và bóng của tháp trên mặt đất dài 20 m. Tính chiều cao của tháp (làm tròn đến mét)
A. 24 m B. 20 m C. 17 m D. 13 m
24. Cho tam giác MNP vuông tại M, đường cao MH. Biết NH = 5 cm, HP = 9 cm. Độ dài MH bằng:
A. 4 B. 4,5 C. 7 D.
25. Giá trị của biểu thức bằng:
Phần II. Tự luận(5 điểm)
Câu 26 (2,5 điểm)
a) So sánh:
b) Tìm điều kiện để có nghĩa.
c) Khử căn ở mẫu
d) Tính giá trị biểu thức
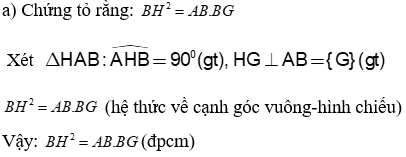
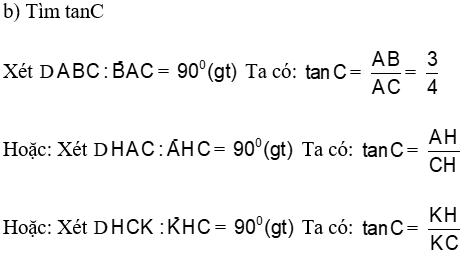
Câu 27(2 điểm): Cho tam giác ABC vuông tại A, AB = 3(cm), AC = 4(cm), đường cao AH. Kẻ HK vuông góc với AC tại K, kẻ HG vuông góc với AB tại G.
Câu 28(0,5 điểm): Giải phương trình
ĐÁP ÁN
I. Phần trắc nghiệm
|
|
|||||||||||||
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
Đ.án |
A |
B |
C |
D |
A |
B |
C |
D |
A |
B |
C |
D |
A |
|
Câu |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
|
Đ.án |
D |
B |
B |
B |
A |
A |
D |
B |
C |
C |
D |
C |
|
II. Phần tự luận
|
Câu |
Lời giải |
Điểm |
|
26 (2,5đ) |
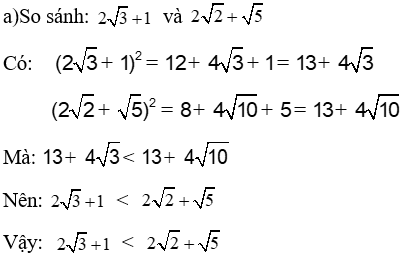 |
0,25
0.25 |
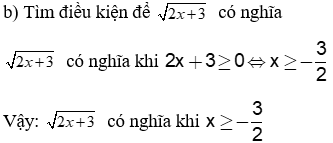 |
0,5 |
|
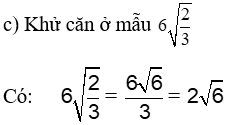 |
0,5 |
|
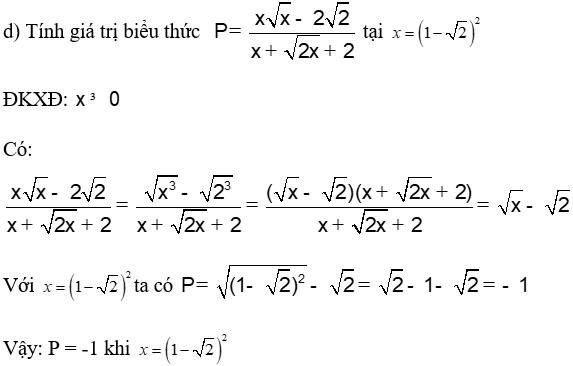 |
0,25
0,5
0,25 |
|
|
27 (2đ) |
|
|
 |
0,25
0,25 |
|
 |
0,5 |
|
 |
0,125
0,125
0,125
0,125 |
|
|
|
0,125
0,125
0,125
0,125 |
|
|
28 (0,5đ) |
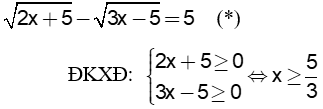 |
0.125 |
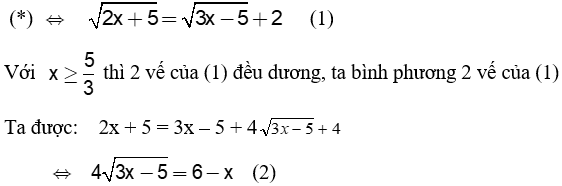 |
0.125 |
|
|
Phương trình (2) có nghiệm khi: 6 – x ≥ 0 ⇔ x ≤ 6 Khi đó: 2 vế của (2) không âm Ta bình phương 2 vế của (2) được 16(3x – 5) = 36 – 12x + x2 ⇔ X2 – 60x + 116 = 0 ⇔ ( x – 2)(x – 58) = 0 |
0.125 |
|
|
Vậy: Tập nghiệm của phương trình là |
0,125 |
Đề số 2
Đề thi Giữa Học kì 1
Năm học 2021 – 2022
Bài thi môn: Toán lớp 9
Thời gian làm bài:60 phút
(không kể thời gian phát đề)
(Đề số 2)
Câu 1:(2 điểm) thực hiện tính:
Câu 2:(1 điểm) Rút gọn
Câu 3:(2 điểm) Tìm x, biết:
a) x2-1=3
Câu 4:(2 điểm) Cho biểu thức:
a)Hãy rút gọn biểu thức P.
b)Tìm giá trị của x để biểu thức P=2
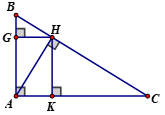
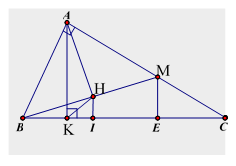
Câu 5:(3 điểm) Cho tam giác ABC vuông tại A có đường cao AK chia cạnh huyền BC thành hai đoạn KB=2cm và KC=6cm.
a)Tính độ dài các đoạn thẳng: AK, AB, AC
b)Trên cạnh AC lấy điểm M ( M khác A và C) Gọi H là hình chiếu của A trên BM. Chứng minh rằng BH.BM=BK.BC
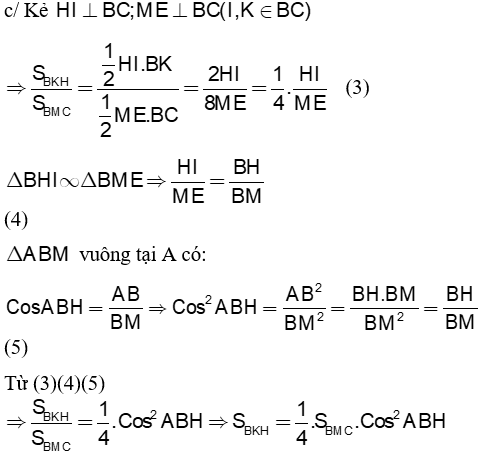
c)Chứng minh rằng:
ĐÁP ÁN
|
CÂU |
ĐÁP ÁN |
ĐIỂM |
|
Câu 1: (2điểm) |
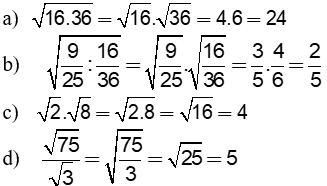 |
0.5 đ 0,5 đ 0,5 đ 0,5 đ |
|
Câu 2: (1,0 điểm) |
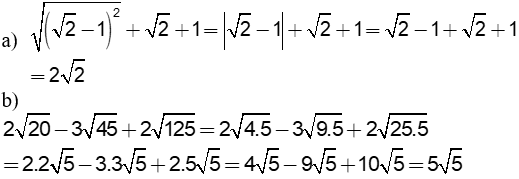 |
0,5 0,5 |
|
Câu 3: |
a) Tìm x, biết x2 -1=3 ⇔ x2 = 4 ⇒ x = -2 hoặc x = 2 Vậy x = -2 hoặc x = 2 |
0,25 0.5 0,25
0,25 0,25
0.25 0.25 |
|
Câu 4: |
Cho biểu thức: a) Hãy rút gọn biểu thức A. b) Tìm giá trị của x để biểu thức P=2 |
0.25 0.25 0.25
0.25
0.25
0.25
0.25
0.25 |
|
Câu 5: |
|
0.25
0,25
0,25
0,25 0.25 0,25 0,25 0,25
0,25
0,25
0,25
0,25
0.25 |
Đề số 3
Đề thi Giữa Học kì 1
Năm học 2021 – 2022
Bài thi môn: Toán lớp 9
Thời gian làm bài:60 phút
(không kể thời gian phát đề)
(Đề số 3)
Bài 1: (1,0 đ) : Tìm điều kiện của x để các căn thức sau có nghĩa.
Bài 2 : (2,0 đ) Tính :
Bài 3 : (1,0 đ) Cho biểu thức
a)Rút gọn A.
b)Tìm x để A = 6
Bài 4 : (2,0 đ): Cho biểu thức
a) Rút gọn biểu thức M
b) Tính giá trị của M khi
c) Tìm giá trị của x để M > 0
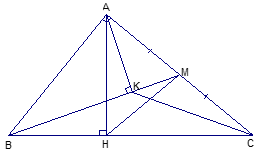
Bài 5 (3,0 đ): Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai đoạn : BH = 4 cm và HC = 6 cm.
a) Tính độ dài các đoạn AH, AB, AC.
b) Gọi M là trung điểm của AC. Tính số đo góc AMB (làm tròn đến độ).
c) Kẻ AK vuông góc với BM (K thuộc BM). Chứng minh : BK.BM = BH.BC
Bài 6 (1,0đ): Giải phương trình sau.
ĐÁP ÁN
|
Bài |
Nội dung |
Điểm |
|
|
1 (1,0 đ) |
1a |
0.5 |
|
|
1b |
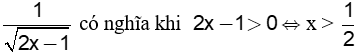 |
0,5 |
|
|
2 (2,0 đ) |
2a |
0,5 |
|
|
2b |
0,5 |
||
|
2c |
|
0.5 |
|
|
2d |
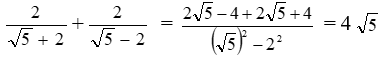 |
0,5 |
|
|
3 (1,0 đ) |
3a |
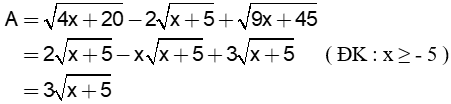 |
0,5 |
|
3b |
|
0,5 |
|
|
4 (2,0 đ) |
4a |
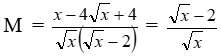 |
0,5 0,5 |
|
4b) |
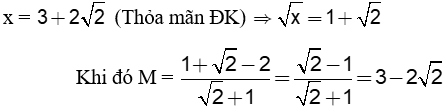 |
0,5 |
|
|
4c) |
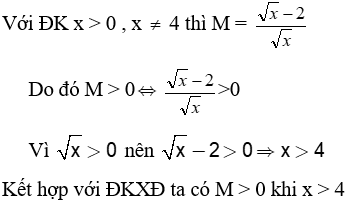 |
0,5 |
|
|
5 (3,0 đ) |
|
0,25
|
|
|
5a |
Tam giác ABC vuông tại A nên : AH2 = HB.HC = 4.6 = 24 => AH = 2√6 (cm) AB2 = BC.HB = 10.4 = 40 => AB = 2√10 (cm) AC2 = BC.HC = 10.6 = 60 => AC = 2√15 (cm) |
0,5 0,75 |
|
|
5b |
ABM vuông tại A |
0,5 0,25 |
|
|
5c |
Δ ABM vuông tại A có AK ⊥ BM => AB2 = BK.BM ΔABC vuông tại A có AH ⊥ BM => AB2 = BH.BC => BK.BM = BH.BC |
0,25 0,25 0,25 |
|
|
6 (1,0 đ) |
KL: Phương trình có nghiệm:x = 2001, y = 2002, z = 2003 |
0,25
0,25 0,25 0,25 |
Đề số 4
Đề thi Giữa Học kì 1
Năm học 2021 – 2022
Bài thi môn: Toán lớp 9
Thời gian làm bài:60 phút
(không kể thời gian phát đề)
(Đề số 4)
Bài 1 (2,0 điểm).
1. Thực hiện phép tính.
2. Tìm điều kiện của x để các biểu thức sau có nghĩa:
Bài 2 (2,0 điểm).
1.Phân tích đa thức thành nhân tử.
2 Giải phương trình:
Bài 3 (2,0 điểm).
Cho biểu thức
a) Rút gọn biểu thức A.
b) Tìm x để
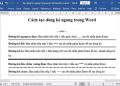
Bài 4 (3,5 điểm).
Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a)Tính độ dài các đoạn thẳng AB, AC, AH.
b)Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC
c)Chứng minh rằng:
Bài 5 (0,5 điểm).
Cho biểu thức P = x3 + y3 – 3(x + y) + 1993.
Tính giá trị biểu thức P với:
……………….. Hết …………………
ĐÁP ÁN
Bài 1
|
Ý |
Nội dung |
Điểm |
|
1.a 0.5đ |
|
0.25 |
|
= 9 – √16 = 9 – 4 = 5 |
0.25 |
|
|
1.b 0.5đ |
|
0.25 |
|
|
0.25 |
|
|
2.a 0.5đ |
Biểu thức |
0.25 |
|
⇔ x ≤ 1 |
0.25 |
|
|
2.b 0.5đ |
|
0.25 |
|
⇔ ( x – 1)2 > 0 ⇔ x ≠ 1 |
0.25 |
Bài 2 (2,0 điểm)
|
Ý |
Nội dung |
Điểm |
|
1.a 0.5đ |
0.25 |
|
|
|
0.25 |
|
|
1.b 0.5đ |
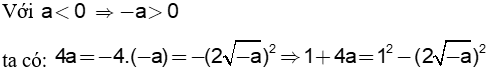 |
0.25 |
|
|
0.25 |
|
|
2 1.0đ |
ĐK 😡 ≥ – 1 |
0.25 |
|
|
0.25 |
|
|
|
||
|
⇔ x + 1 = 25 ⇔ x = 24 ( T/m ĐKXĐ) |
0.25 |
|
|
Vậy phương trình có nghiệm duy nhất x = 24 |
0.25 |
Bài 3 (2,0 điểm).
|
Ý |
Nội dung |
Điểm |
|
a 1.25đ |
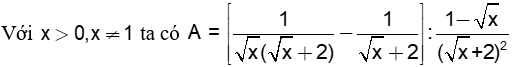 |
0.25 |
|
|
0.25 |
|
|
|
0.25 |
|
|
|
0.25 |
|
|
Vậy |
0.25 |
|
|
b 0.75đ |
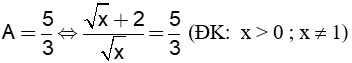 |
0.25 |
|
|
||
|
0.25 |
||
|
Vậy với x = 9 thì . |
0.25 |
Bài 4 (3,5 điểm).
|
Ý |
Nội dung |
Điểm |
|
a 1.5đ |
|
|
|
+ ΔABC vuông tại A, đường cao AH => AB2 = BH.BC = 2.8 = 16 |
0.25 |
|
|
=> AB = 4 cm ( Vì AB > 0 ) |
0.25 |
|
Ý |
Nội dung |
Điểm |
|
+ BC2 = AB2 + AC2 (Định lý Pitago trong tam giác vuông ABC) |
0.25 |
|
|
|
0.25 |
|
|
+ Có HB + HC = BC HC = BC – HB = 8 – 2 = 6 cm AH2 = BH.CH = 2.6 – 12 |
0.25 |
|
|
=> AH = √12 = 2√3 cm ( Vì AH > 0) |
0.25 |
|
|
b 1.0đ |
+ Δ ABK vuông tại A có đường cao AD => AB2 = BD.BK (1) |
0.5 |
|
+ Mà AB2 = BH.BC ( Chứng minh câu a) (2) |
0.25 |
|
|
Từ (1) và (2) => BD.BK = BH.BC |
0.25 |
|
|
c 1.0đ |
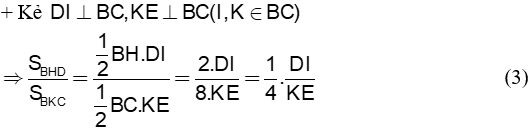 |
0.25 |
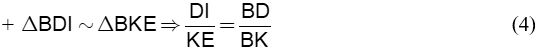 |
0.25 |
|
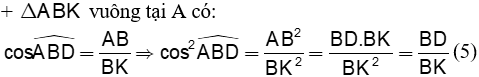 |
0.25 |
|
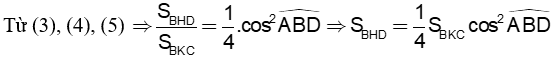 |
0.25 |
Bài 5 (0,5 điểm).
|
Ý |
Nội dung |
Điểm |
|
0.5đ |
Ta có: x3 = 18 + 3x => x3 – 3x =18 y3 = 6 + 3y => y3 – 3y = 6 |
0.25 |
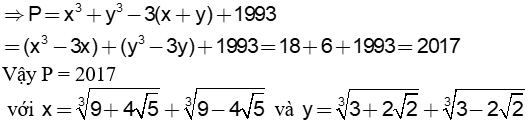 |
0.25 |
Trên đây là tổng hợp các đề thi giữa kỳ 1 toán 9 đầy đủ có đáp án chi tiết nhất. Hy vọng qua bài viết sẽ giúp các em học sinh có dễ dàng làm quen với đề và đạt được kết quả cao nhất trong kỳ thi.


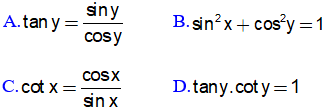
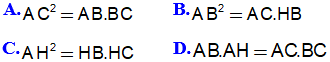






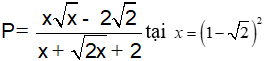


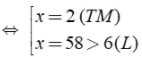
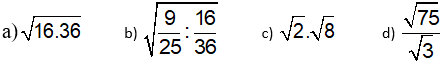

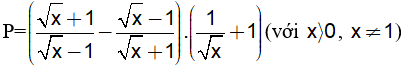
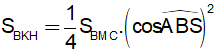
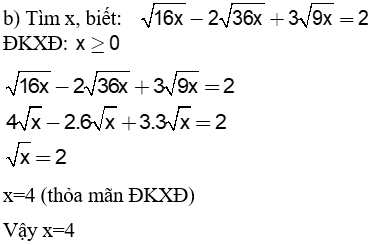
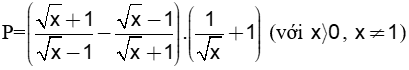
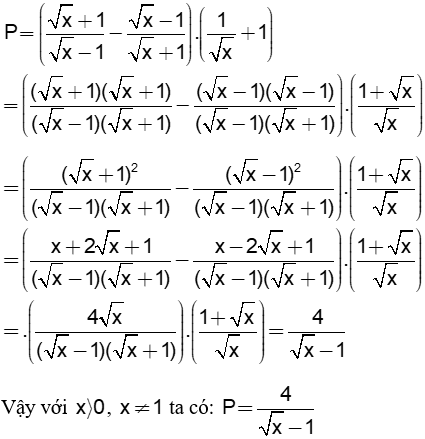
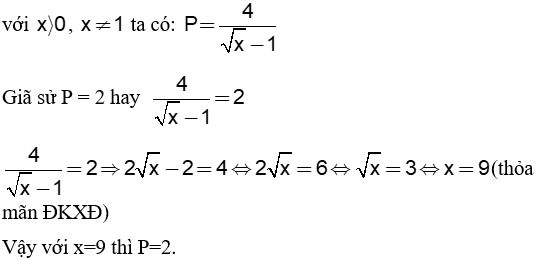


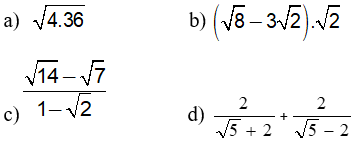
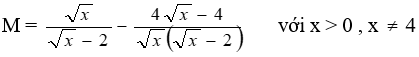
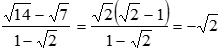
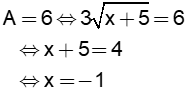
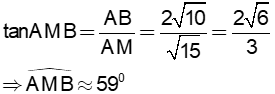
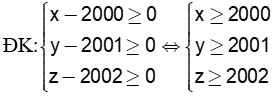

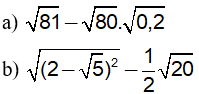

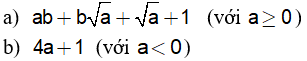
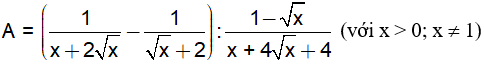
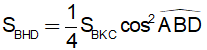
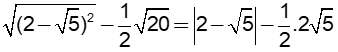
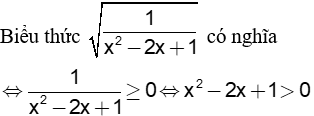
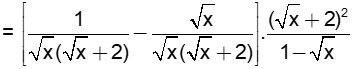
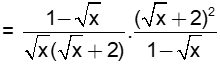
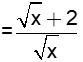
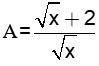 (với x > 0; x ¹ 1)
(với x > 0; x ¹ 1)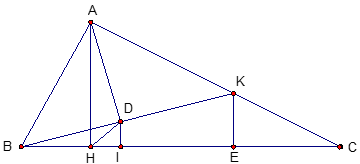






![50+ Đề thi học kì 2 Toán 11 năm 2022 mới nhất [Có đáp án]](https://seolalen.vn/wp-content/uploads/2022/09/de-thi-hoc-ky-2-lop-11-mon-toan-120x86.jpg)