Bạn đang cần tìm tài liệu ôn tập toán hình 7 nhưng lại không tìm thấy tài liệu ở đâu đầy đủ, chi tiết miễn phí. Đừng lo lắng, hãy theo dõi bài viết dưới đây. Vì ngay trong bài viết này, chúng tôi sẽ cung cấp đến bạn trọn bộ tài liệu ôn tập đầy đủ, kèm lời giải chi tiết. Mời các bạn tham khảo!
Các dạng toán hình học lớp 7
Giới thiệu Tài liệu các dạng toán hình học lớp 7
Chú ý:
– Với n đường thẳng phân biệt giao nhau tại một điểm có 2n tia chung gốc. Số góc tạo bởi hai tia chung
gốc là: 2n(2n-1) : 2 = n( 2n – 1). Trong đó có n góc bẹt. Số góc còn lại là 2n(n – 1). Số cặp góc đối
đỉnh là: n(n – 1).
– Hai góc bù nhau là hai góc có tổng bằng 1800, hai góc phụ nhau là hai góc có tổng bằng 900, góc bẹt là góc có số đo bằng 1800, góc tù là góc có số đo nằm trong khoảng từ 900 đến 1800, góc vuông = 900, góc nhọn có số đo nằm trong khoảng 00 đến 900
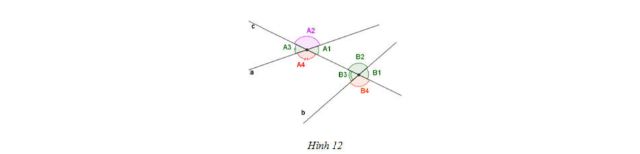
– Khi một đường thẳng cắt hai đường thẳng sẽ tạo ra các cặp góc sole trong, sole ngoài, đồng vị, trong cùng
phía.
– Các cặp góc sole trong: A1 và B3; A4 và B2.
– Các cặp góc sole ngoài: A3 và B1; A2 và B4.
– Các cặp góc đồng vị: A2 và B2; A1 và B1;A3 và B3; A4 và B4.
– Các cặp góc trong cùng phía : A1 và B2; A4 và B3.
– Các cặp góc ngoài cùng phía: A2 và B1; A3 và B4.
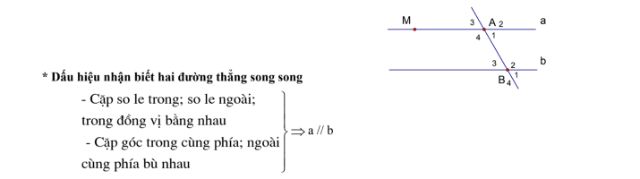
3. Hai đường thẳng song song: Hai đường thẳng song song thì các cặp góc sole trong bằng nhau, các cặp góc sole ngoài bằng nhau, các cặp góc đồng vị bằng nhau, các cặp góc trong cùng phía, ngoài cùng phía
bù nhau.
– Có a // b ; c ∩ a = {A}; c ∩ b = {B}
7. Các trường hợp bằng nhau của tam giác
*Trường hợp 1 : Cạnh – cạnh – cạnh
– Nếu 3 cạnh của tam giác này bằng 3 cạnh của tam giác kia thì hai tam giác đó bằng nhau.
*Trường hợp 2 : Cạnh – góc – cạnh
– Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai
tam giác đó bằng nhau.
*Trường hợp 3 : Góc – cạnh – góc
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam
giác đó bằng nhau.
8. Các trường hợp bằng nhau của tam giác vuông.
*Trường hợp 1 : Hai cạnh góc vuông
– Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác vuông kia thì
hai tam giác vuông đó bằng nhau.
*Trường hợp 2 : Cạnh góc vuông và góc nhọn kề
– Nếu một cạnh góc vuông và góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và
góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
*Trường hợp 3 : Cạnh huyền và góc nhọn
– Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam
giác vuông kia thì hai tam giác vuông đó bằng nhau.
*Trường hợp 4 : Cạnh huyền và cạnh góc vuông
– Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc
vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
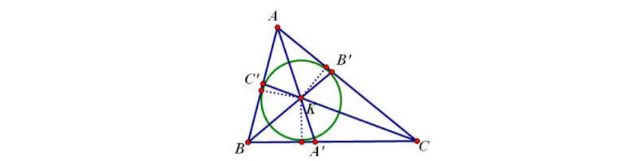
b) Đường phân giác trong tam giác: Là đường chia góc trong tam giác thành 2 phần bằng nhau. Ba đường
phân giác cắt nhau tại một điểm là tâm đường tròn nội tiếp tam giác ( đường tròn tiếp xúc trong với 3 cạnh của
tam giác). Tâm đường tròn nội tiếp tam giác cách đều 3 cạnh tam giác.
– Một điểm nằm trên đường phân giác của một góc luôn có khoảng cách tới hai cạnh bằng nhau.
– Phân giác trong và phân giác ngoài của một góc vuông góc với nhau.
– Trong một tam giác, hai đường phân giác ngoài của hai góc đồng quy với đường phân giác trong của góc còn lại.
Tính chất: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó. Nếu một điểm nằm bên
trong một góc và cách đều hai cạnh của góc đó thì nó nằm trên tia phân giác của góc đó.
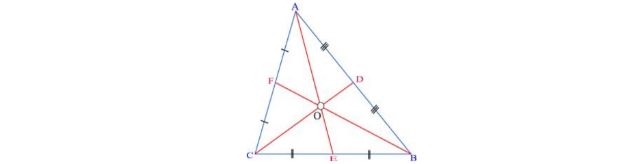
c) Đường trung tuyến trong tam giác: Là đường kẻ từ đỉnh đến trung điểm cạnh đối diện. Ba đường trung tuyến đồng quy tại một điểm là trọng tâm tam giác.
Nếu O là trọng tâm tam giác thì 2OE=OA; 2OD=OC; 2OF=OB
d)Đường trung trực trong tam giác: Là đường đi qua trung điểm của đoạn thẳng và vuông góc với đoạn thẳng đó. Ba đường trung trực trong tam giác đồng quy tại 1 điểm là tâm đường tròn ngoại tiếp tam giác ( Đường tròn đi qua 3 đỉnh của tam giác).
– Một điểm bất kì nằm trên trung trực luôn cách đều hai đầu mút của đoạn thẳng.
e) Đường trung bình trong tam giác: Là đường đi qua trung điểm của 2 cạnh bên tam giác. Đường trung bình song song và bằng một nửa cạnh đáy.
CÁC CHÚ Ý ĐẶC BIỆT
– Trong tam giác cân, đường cao, đường trung tuyến, trung trực, phân giác của đỉnh cân là một.
– Trong tam giác đều, tất cả các đường từ một đỉnh là một.
– Trong tam giác vuông: đường trung tuyến bằng một nửa cạnh huyền, cạnh đối diện với góc 300 cũng có
độ lớn bằng nửa cạnh huyền.
MỘT SỐ PHƯƠNG PHÁP HAY DÙNG TRONG HÌNH HỌC 7
1. Các phương pháp chứng minh định lý :
Muốn chứng minh định lý ” Nếu A thì B ” ( ký hiệu A ⇒B) ta có thể dùng một trong những phương
pháp sau đây :
2. Chứng minh rằng từ A ta suy ra C rồi từ C ta suy ra B .
Phương pháp này gọi là phương pháp: chứng minh trực tiếp .
3. Giả sử A ta suy ra B ( B có nội dung trái ngược với B ) ta dẫn đến một điều vô lý . Vậy giả sử trên là
sai, nghĩa là từ A suy ra B là đúng .
Phương pháp này gọi là phương pháp: chứng minh phản chứng .
4. Các phương pháp chứng minh hai góc là đối đỉnh :
Muốn chứng minh hai góc xOy và x’Oy’ là hai góc đối đỉnh ta có thể dùng một trong những phương pháp sau đây :
5. Chứng minh rằng tia Ox là tia đối của tia Ox’ ( hoặc Oy’ ) và tia Oy là tia đối của tia Oy’ ( hoặc Ox’ ), tức là hai cạnh của một góc là tia đối của hai cạnh của góc kia ( định nghĩa ).
6. Chứng minh rằng ∠ xOy = ∠ x’Oy’ ; tia Ox và tia Ox’ đối nhau còn hai tia Oy và tia Oy’ nằm trên hai
nửa mặt phẳng đối nhau có bờ là đường thẳng xx’ (hệ quả của định nghĩa ).
7. Các phương pháp chứng minh một điểm là trung điểm của một đoạn thẳng.
Muốn chứng minh rằng điểm B là trung điểm của đoạn thẳng AC ta có thể dùng một trong những phương pháp sau đây:
Bạn có thể tải tài liệu chi tiết các dạng toán hình học lớp 7 TẠI ĐÂY
15 Bài toán hình ôn Học kì 1 lớp 7
Giới thiệu 15 bài toán hình ôn Học kì 1 lớp 7
c/. Chứng minh BN // AC :
Ta có : ABM = CDM (cmt) AB = CD (cạnh tương ứng)
Mà : CD = CN (gt) AB = CN
Xét ABC và NCB , ta có :AB = CN (cmt); BC cạnh chung.
ABC = NCB (c – g – c) Mà : (so le trong) BN // AC
BÀI 2 :
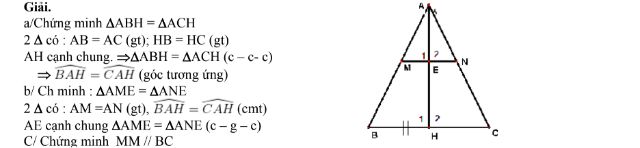
Cho tam giác ABC có AB = AC, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho AM = AN.
Gọi H là trung điểm của BC.
a/ Chứng minh : ABH = ACH.
b/ Gọi E là giao điểm của AH và NM. Chứng minh : AME = ANE
c/ Chứng minh : MM // BC.
Ta có : ABH = ACH (cmt) Mà : (hai góc kề bù)
Hay BC AH
Chứng minh tương tự, ta được : MN AE hay MN AH MM // BC.
Bài 3 :
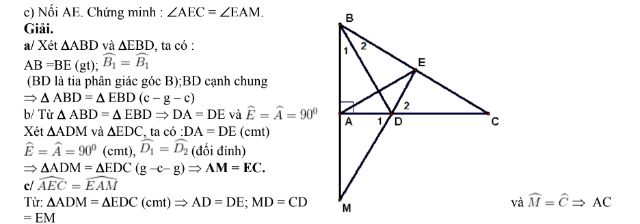
Cho tam giác ABC vuông tại A. tia phân giác của góc ABC cắt AC tại D. lấy E trên cạnh BC sao cho BE =AB.
a) Chứng minh : ABD =
b) Tia ED cắt BA tại M. chứng minh : EC = AM
Xét AEM và EAC, ta có:AM = EC (cmt), ; AC = EM
AEM =EAC (c g c) (ĐPCM)
BÀI 4 :
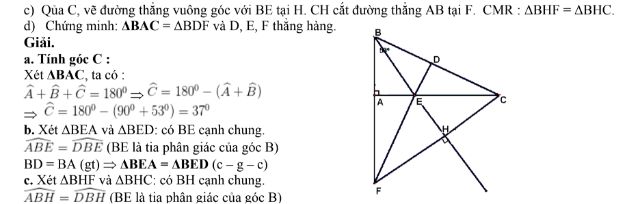
Cho tam giác ABC vuông góc tại A có góc B = 530
a) Tính góc C.
b) Trên cạnh BC, lấy điểm D sao cho BD = BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh : ΔBEA = ΔBED.
ΔBHF = ΔBHC (cạnh huyền – góc nhọn)
BF = BC (cạnh tương ứng) ΔBHF = ΔBHC
d. ΔBAC = ΔBDF và D, E, F thẳng hàng
xét ΔBAC và ΔBDF: có:BC = BF (cmt); Góc B chung;.BA = BC (gt) ΔBAC = ΔBDF
Mà : (gt) hay BD DF (1)
Mặt khác : (hai góc tương ứng của ΔBEA = ΔBED); Mà (gt)
hay BD DE (2)
Từ (1) và (2), suy ra : DE trùng DF Hay : D, E, F thẳng hàng. (ĐPCM)
BÀI 5
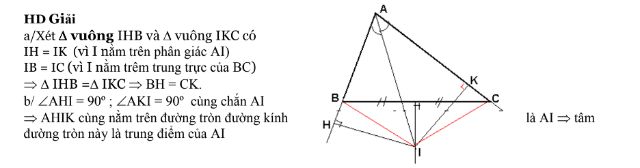
Cho tam giác ABC (AB <AC). Tia phân giác của góc A cắt đường trung trực của BC tại I. kẻ IH vuông góc
AB tại H. IK vuông góc AC tại K.
a/ Chứng minh : BH = CK.
b/ Chứng minh AHIK nội tiếp đường tròn và tim tâm đường tròn đó
II. PHẦN ỨNG DỤNG THỰC HÀNH
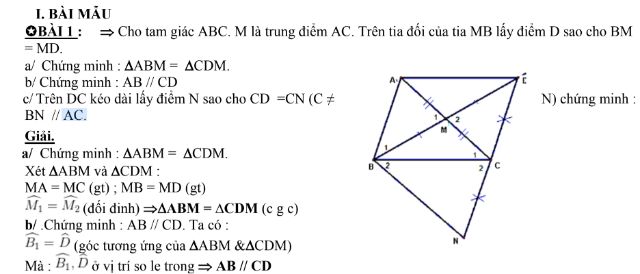
BÀI 1 :
Cho ABC có Â = 900. Tia phân giác BD của góc B(D thuộc AC). Trên cạnh BC lấy điểm E sao cho BE =BA.
a) So sánh AD và DE
b) Chứng minh:
c) Chứng minh : AE BD
BÀI 2 :
Cho ΔABC nhọn (AB < AC). Gọi M là trung điểm của BC. Trên tia AM lấy điểm N sao cho M là trung
điểm của AN.
a/. Ch/m :Δ AMB = ΔNMC
b/. Vẽ CD AB (D AB). So sánh góc ABC và góc BCN. Tính góc DCN.
c/. Vẽ AH BC (H BC), trên tia đối của tia HA lấy điểm I sao cho HI = HA.
Ch/m : BI = CN.
BÀI 3 :
Vẽ góc nhọn xAy. Trên tia Ax lấy hai điểm B và C (B nằm giữa A và C). Trên tia Ay lấy hai điểm D và E
sao cho AD = AB; AE = AC
a) Chứng minh BE = DC
b) Gọi O là giao điểm BE và DC. Chứng minh tam giác OBC bằng tam giác ODE.
c) Vẽ trung điểm M của CE. Chứng minh AM là đường trung trực của CE.
Bài 4.
Cho tam giác ABC ( AB< AC ) . Gọi I là trung điểm của AC. Trên tia đối của tia IB lấy điểm D, sao cho IB
= ID. Chứng minh :
a) Tam giác AIB bằng tam giác CID.
b) AD = BC v à AD // BC.
BÀI 5.
Cho tam giác ABC có góc A =350. Đường thẳng AH vuông góc với BC tại H. Trên đường vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH = BD.
a) Chứng minh ΔAHB = ΔDBH.
b) Chứng minh AB//HD.
c) Gọi O là giao điểm của AD và BC. Chứng minh O là trung điểm của BH.
d) Tính góc ACB , biết góc BDH= 350
Bài 6 :
Cho tam giác ABC cân tại A và có .
- Tính và
- Lấy D thuộc AB, E thuộc AC sao cho AD = AE. Chứng minh : DE // BC.
Bài 7 :
Cho tam giác ABC cân tại A. Lấy D thuộc AC, E thuộc AB sao cho AD = AE.
- Chứng minh : DB = EC.
- Gọi O là giao điểm của BD và EC. Chứng minh : OBC và ODE là cân.
- Chứng minh rằng : DE // BC.
Bài 8 :
Cho tam giác ABC. Tia phân giác của góc C cắt AB tại D. trên tia đối của tia CA lấy điểm E sao cho CE =CB.
- Chứng minh : CD // EB.
- Tia phân giác của góc E cắt CD tại F. vẽ CK vuông góc EF tại K. chứng minh : CK Tia phân giác của góc ECF.
Bài 9 :
Cho tam giác ABC vuông tại A có . Vẽ Cx vuông góc BC, trên tia Cx lấy điểm E sao cho CE = CA (CE , CA nằm cùng phía đối BC). trên tia đối của tia BC lấy điểm F sao cho BF = BA. Chứng minh :
- Tam giác ACE đều.
- A, E, F thẳng hàng.
Bài 10 :
Cho tam giác ABC vuông góc tại A có góc B = 75o; BC = 10 cm .
a) Tính góc C.
b) Trên cạnh BA kéo dài về phía A đoạn AD = AB, Tính diện tích ABD
(Gợi ý: Hạ đường cao sẽ có vuông với góc nhọn = 30o )
Bạn có thể tải tài liệu các bài toán hình lớp 7 ôn tập học kỳ TẠI ĐÂY
Chuyên đề: PHƯƠNG PHÁP TAM GIÁC BẰNG NHAU
Môn: Hình học
Lớp: 7
I. Mục tiêu
Sau khi học xong chuyên đề học sinh có khả năng:
1.Biết vận dụng các trường hợp bằng nhau của tam giác để chứng minh hai
tam giác bằng nhau; Nắm được các bước chứng minh hai đoạn thẳng hay hai góc
bằng nhau; Biết vẽ thêm đường phụ để tạo ra hai tam giác bằng nhau.
- Hiểu các bước phân tích bài toán, tìm hướng chứng minh
- Có kĩ năng vận dụng các kiến thức được trang bị để giải toán.
II. Các tài liệu hỗ trợ:
– Bài tập nâng cao và một số chuyên đề toán 7
-Hình học nâng cao THCS
– Vẽ thêm yếu tố phụ để giải các bài toán hình học 7
– Bồi dưỡng toán 7
– Nâng cao và phát triển toán 7
– …
III. Nội dung
1. Kiến thức cần nhớ
Ta đã biết nếu hai tam giác bằng nhau thì suy ra được các cặp cạnh tương ứng
bằng nhau, các cặp góc tương ứng bằng nhau. Đó là lợi ích của việc chứng minh hai
tam giác bằng nhau.
*. Các trường hợp bằng nhau của tam giác
a, Trường hợp cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba
cạnh tương ứng của tam giác kia thì hai tam giác đó bằng nhau.
b, Trường hợp cạnh – góc – cạnh: Nếu hai cạnh và một góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng
nhau
c, Trường hợp góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác
này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
*. Muốn chứng minh hai đoạn thẳng(hay hai góc) bằng nhau ta thường làm theo các bước sau:
– Xét xem hai đoạn thẳng(hay hai góc) là hai cạnh (hay hai góc) thuộc hai
tam giác nào.
– Chứng minh hai tam giác đó bằng nhau
– Suy ra hai cạnh (hay hai góc) tương ứng bằng nhau.
*. Để tạo ra được hai tam giác bằng nhau, có thể ta phải vẽ thêm đường phụ bằng nhiều cách:
– Nối hai cạnh có sẵn trên hình để tạo ra một cạnh chung của hai tam giác.
– Trên một tia cho trước, đặt một đoạn bằng một đoạn thẳng khác.
– Từ một điểm cho trước, vẽ một đường thẳng song song với một đoạn thẳng.
– Từ một điểm cho trước, vẽ một đường thẳng vuông góc với một đoạn thẳng.
Ngoài ra còn nhiều cách khác ta có thể tích luỹ được kinh nghiệm khi giải
nhiều bài toán.
2. Các ví dụ:
2.1. Ví dụ 1(BTNC&MSCĐ/123)
Cho góc vuông xOy, điểm A trên tia Ox, điểm B trên tia Oy. Lấy điểm E trên
tia đối của tai Ox, điểm F trên tia Oy sao cho OE= OB, OF= OA.
a, Chứng minh AB = EF, AB vuông góc EF.
Từ (*) và(**)
VOMN vuông cân
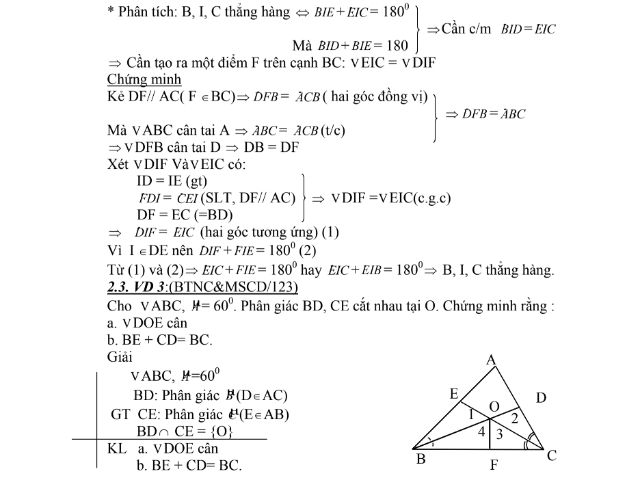
2.2. VD2( BT26/VTYTP/62):
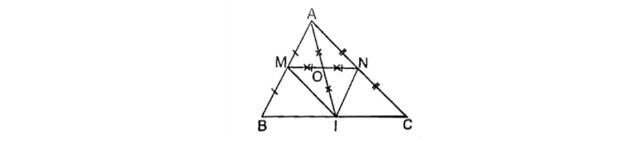
Cho V ABC cân đỉnh A. Trên cạnh AB lấy điểm D, trên tia đối của tia CA lấy
điểm E sao cho BD = CE. Nối D với E. Gọi I là trung điểm của DE.
Chứng minh ba điểm B, I, C thẳng hàng.
Bạn có thể tải chi tiết Chuyên đề: PHƯƠNG PHÁP TAM GIÁC BẰNG NHAU: TẠI ĐÂY
Sách ôn tập Hình học lớp 7

Cuốn ôn tập Hình Học 7 được nhà xuất bản giáo dục Việt Nam phát hành và do hai tác giả là Nguyễn Ngọc Đạm, Vũ Dương Thụy viết. Cuốn sách gồm 3 chương tất cả đó là: I. Đường thẳng vuông góc, đường thẳng song song; 2. Tam Giác; 3. Quan hệ giữa các yếu tố trong tam giác, Các đường đồng quy trong tam giác.
Các bạn có thể tải sách: TẠI ĐÂY
Chuyên đề toán lớp 7 – Hình học: đường tròn, tam giác
Giới thiệu chuyên đề toán 7
A. Lý thuyết
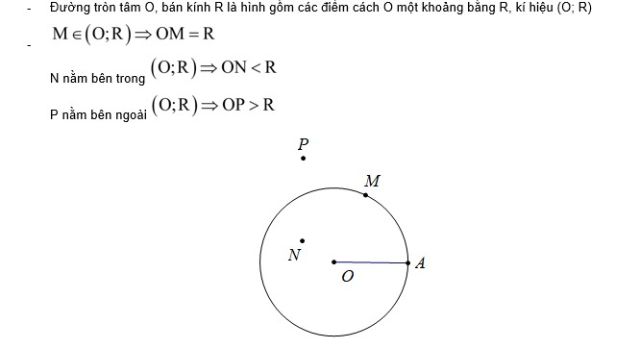
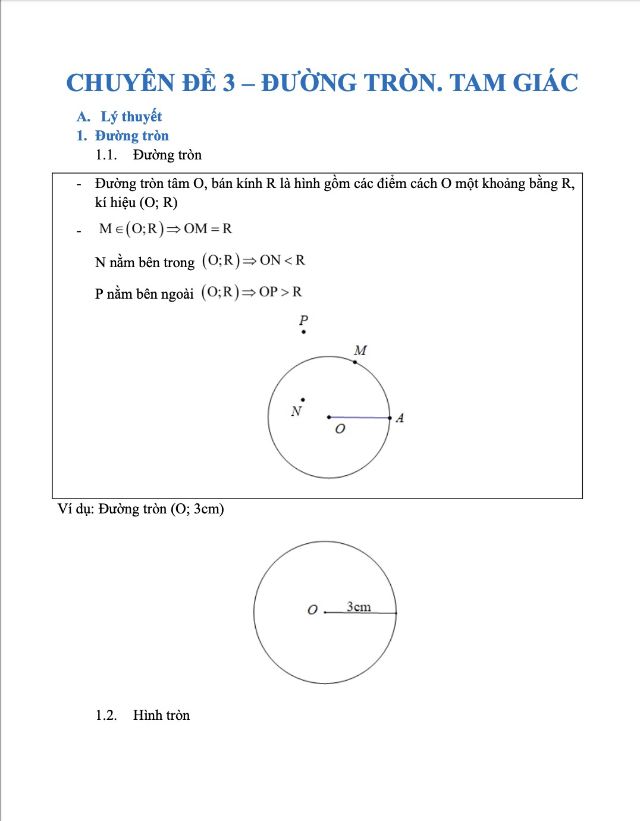
1. Đường tròn
- Đường tròn
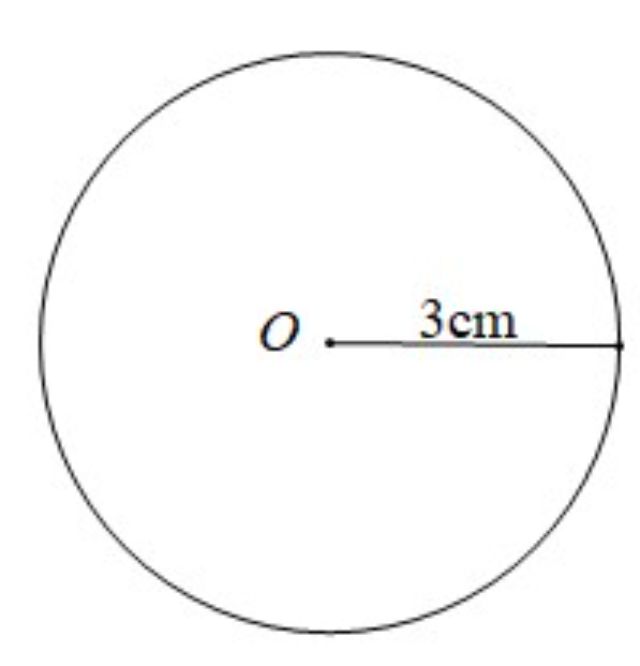
Ví dụ: Đường tròn (O; 3cm)
- Hình tròn
|
– Hình tròn là hình gồm các điểm nằm trên đường tròn và các điểm nằm trong đường tròn đó. |
Ví dụ: Cái đĩa, đồng hồ, …
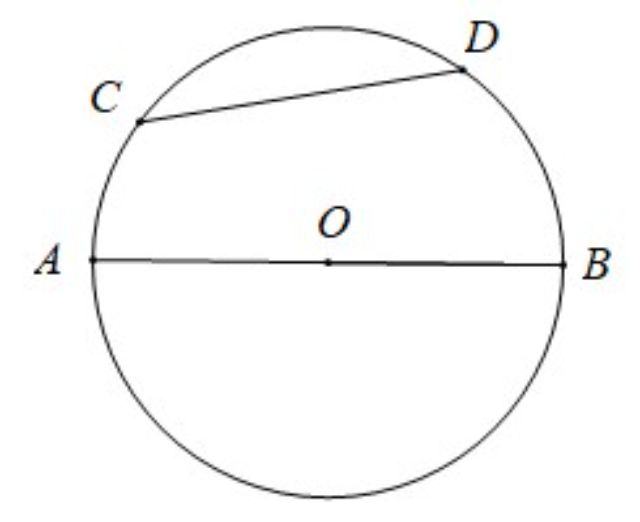
- Dây cung
|
– Hai điểm C, D của một đường tròn chia đường tròn thành hai cung. Đoạn thẳng nối hai mút của một cung là dây cung. Dây cung đi qua tâm là đường kính. |
Ví dụ: Đoạn thẳng CD là dây cung, đoạn thẳng AB là đường kính.
2. Tam giác
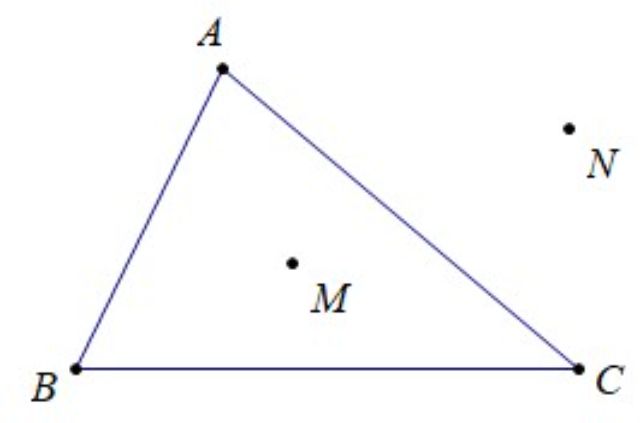
- Định nghĩa
|
– Tam giác ABC là hình gồm ba đoạn thẳng AB, BC, CA khi A, B, C không thẳng hàng. – Điểm M là điểm nằm trong tam giác, điểm N là điểm nằm ngoài tam giác. |
- Các yếu tố
B. Bài tập:
DẠNG 1: ĐƯỜNG TRÒN
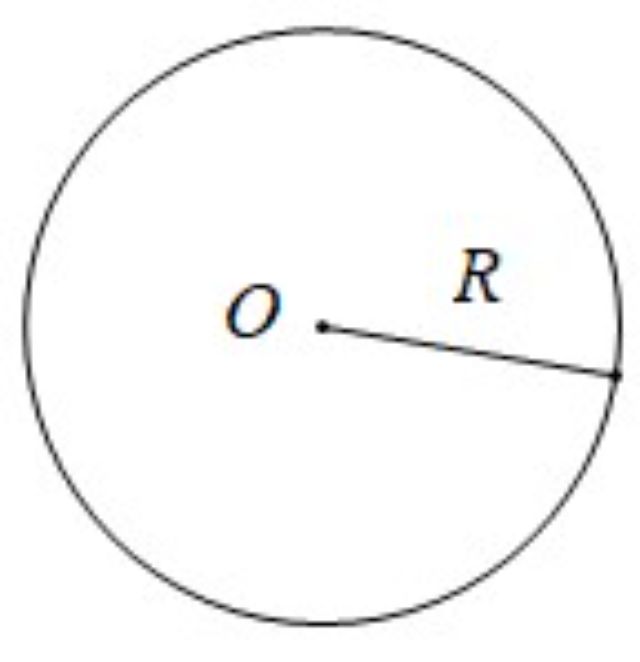
Bài toán 1: Trên hình bên, ta có đường tròn (O; R)
|
 |
Bài toán 2:
a. Những điểm cách A một khoảng 1,5cm thì nằm ở đâu? Những điểm cách B một khoảng 2cm thì nằm ở đâu?
b. Có điểm nào vừa cách A là 1,5cm; vừa cách B là 2cm không?
Bài toán 3: Cho đoạn thẳng AB = 3cm
a. Vẽ đường tròn (A; 1,5cm) và đường tròn (B; 1cm). Hỏi có điểm nào vừa cách A là 1,5cm; vừa cách B một khoảng 1cm;
b. Hãy nêu bước vẽ điểm M vừa cách A là 3cm, vừa cách B là 3cm.
Bài toán 4: Cho đoạn thẳng AB = 4cm. Hãy dựng đường tròn tâm O nhận AB làm đường kính.
Bài toán 5: Cho AB = 3cm, vẽ đường tròn (A; 2,5cm) và đường tròn (B; 1,5cm), hai đường tròn này cắt nhau tại 2 điểm C, D
a. Tính độ dài đoạn thẳng CA, CB, DA, DB;
b. Tại sao đường tròn (B; 1,5cm) lại cắt đoạn thẳng AB tại trung điểm I của AB?
Đường tròn (A; 2,5cm) cắt đoạn thẳng AB tại K. Tính độ dài KB.
Bài toán 6: Vẽ đường tròn tâm O bán kính 2cm. Gọi M là một điểm nằm ngoài đường tròn tâm O; OM cắt đường tròn (O; 2cm) ở I, biết OM = 3cm.
a, Tính IM
b, Vẽ đường tròn tâm I bán kính IM. Chứng tỏ điểm O nằm ngoài đường tròn (I; IM)
c, Đường tròn (I; IM) cắt đường tròn (O; 2cm) ở P và Q, cắt OM ở K. Chứng tỏ rằng điểm K nằm trong đường tròn (O; 2cm).
Bài toán 7: Cho hai điểm A, B cách nhau 3cm. Vẽ đường tròn (A; 2,5cm) và đường tròn (B; 1,5cm). Hai đường tròn này cắt nhau tại hai điểm C và D.
a, Tính CA và DB.
b, Tại sao (B; 1,5cm) cắt đoạn thẳng AB tại trung điểm I của AB.
c, Đường tròn (A; 2,5cm) cắt đoạn thẳng AB tại K. Tính KB.
Bài toán 8: Cho đoạn thẳng AB = 6cm. Vẽ đường tròn (A; 5cm) và đường tròn (B; 3cm). Hai đường tròn này cắt nhau tại M và N, các đường tròn tâm A và B theo thứ tự cắt đoạn thẳng AB tại C và D
a, Tính AM, BM
b, Chứng minh rằng D là trung điểm của đoạn AB
c, Tính độ dài CD
b, Trên hình vẽ có bao nhiêu dây cung, dây cung nào lớn nhất. Hãy kể tên
c, Lấy điểm D và E sao cho OD = 1,5cm, OE = 3cm. Hãy xác định vị trí của điểm D và E đối với đường tròn tâm O bán kính bằng 2 cm.
Bài toán 10: Vẽ đường tròn (O; 2cm);
a, Lấy điểm A bất kì trên đường tròn (O; 2cm), vẽ đường tròn (A; 2cm ), đường tròn này cắt đường tròn tâm O ở trên tại 2 điểm C, D;
b, Vẽ đường tròn (C; 2cm);
c, Chứng tỏ rằng đường tròn (C; 2cm) đi qua 2 điểm O, A.
DẠNG 2: TAM GIÁC
Bài toán 11: Vẽ tam giác ABC có:
Bài toán 13: Cho bốn điểm A, B, C, D trong đó không có ba điểm nào thẳng hàng. Cứ qua ba điểm vẽ một tam giác. Hỏi vẽ được mấy tam giác, là những tam giác nào?
a, d không cắt một cạnh nào của tam giác?
b, d cắt cả ba cạnh của tam giác
d) Trên cạnh AB lấy điểm E (E không trùng với A và B). Chứng minh rằng 2 đoạn thẳng BD và CE cắt nhau.
Bài toán 18: Vẽ ΔABC. Lấy M là điểm trong của ΔABC. Vẽ các tia AM, BM, CM cắt các cạnh của ΔABC tương ứng tại các điểm N, P, Q. Vẽ ΔNPQ. Hỏi điểm M có nằm trong ΔNPQ hay không?
Bài toán 19: Vẽ hình để thấy được mỗi câu sau đây là sai
a) Hình gồm 3 đoạn thẳng được gọi là tam giác
b) Hình gồm 3 đoạn thẳng đôi một cắt nhau được gọi là tam giác.
c) Hình gồm 3 đoạn thẳng đôi một cắt nhau tạo ra 3 giao điểm (phân biệt) được gọi là tam giác.
d) Hình gồm 3 đoạn thẳng AB, BC, CA được gọi là tam giác ABC.
e) Hình gồm 3 điểm không thẳng hàng A, B, C được gọi là tam giác ABC.
f) Một điểm không thuộc cạnh của tam giác ABC thì phải nằm trong tam giác đó.
g) Một điểm không phải là đỉnh của tam giác ABC thì phải nằm trong tam giác đó.
h) Một điểm không nằm bên trong tam giác ABC thì phải nằm ngoài tam giác đó.
i) Hình gồm 2 góc được gọi là tam giác.
j) Hình gồm 3 góc mà các cạnh của nó đôi một cắt nhau tạo ra ba điểm được gọi là tam giác.
Bạn có thể tải bản PDF: TẠI ĐÂY
Hình học lớp 7: Chuyên đề: Hai đường thẳng vuông góc
Bạn có thể tải bản PDF: TẠI ĐÂY
Tổng hợp đề kiểm tra 1 tiết môn Toán hình lớp 7 – Trường THCS Hành Minh
Bạn có thể tải bản PDF: TẠI ĐÂY
Đề cương ôn tập chương 1 phần Hình học – môn Toán lớp 7
ĐỀ CƯƠNG ÔN TẬP CHƯƠNG 1 PHẦN HÌNH HỌC
MÔN: TOÁN LỚP 7
I. LÝ THUYẾT
10 câu hỏi ôn tập chương I (trang 102 SGK)
II. BÀI TẬP
- Các bài: 55; 56; 57; 58; 59; 60 (SGK – trang 103-104)
- Bài tập thêm:
Bài 1: Cho hình vẽ, hãy tìm x.
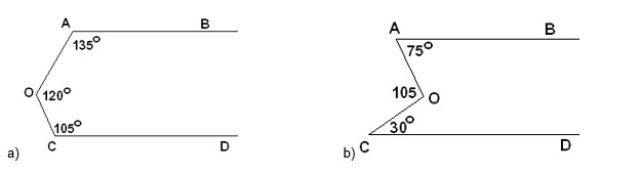
Bài 2: Cho hình vẽ, hãy chứng minh AB//CD
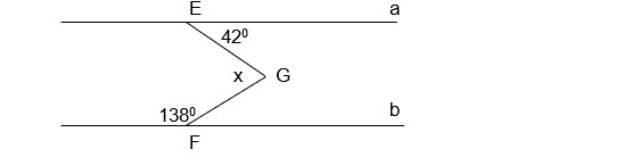
Bài 3: Cho hình vẽ biết a//b. Hãy tính x?
Bài 7: Chứng minh rằng hai tia phân giác của hai góc kề bù thì vuông góc với nhau.
Bài 8: Cho góc xOy và góc yOz là hai góc kề bù. Tia Om là phân giác của góc xOy. Trên cùng một nửa mặt phẳng bờ xz chứa tia Oy, vẽ tia On sao cho: On vuông góc với Om. Chứng minh rằng: Tia On là tia phân giác của góc yOz.
b) Qua A vẽ d//BC, Chứng minh rằng: ++=1800
Bạn có thể tải bản PDF: TẠI ĐÂY
Đề cương ôn tập chương 2 phần Hình học môn Toán lớp 7
ĐỀ CƯƠNG ÔN TẬP CHƯƠNG 2 PHẦN HÌNH HỌC
MÔN: TOÁN LỚP 7
A . Lý thuyết: Các câu hỏi ôn tập chương II (SGK _ tr 139|)
- Bài tập:
_ Các bài tập ôn tập chương : 67 => 73 (SGK _ tr 140_141)
_ Các bài tập ôn tập chương : 103 =>108(SBT _ tr 110_ 111)
Bài tập bổ sung:
Bài 1:
b)Gọi M là trung điểm của BC. Chứng minh rằng AM là tia phân giác góc DAE.
c)Từ B và C vẽ BH và CK theo thứ tự vuông góc với AD và AE. CMR: BH = CK.
a, Tính MC, MD, CD
b, Tam giác MCD là tam giác vuông không? Tại sao?
Bạn có thể tải bản PDF: TẠI ĐÂY
Những tài liệu mà chúng tôi cung cấp trên đều là những tài liệu mà Seo Là Lên tổng hợp được. Mong rằng những tài liệu toán hình 7 trên đều có ích với bạn. Trân Trọng!







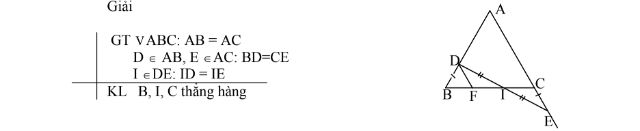


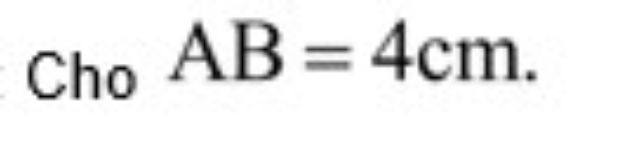





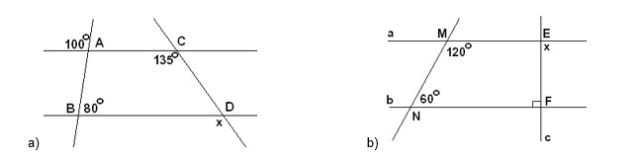














![50+ Đề thi học kì 2 Toán 11 năm 2022 mới nhất [Có đáp án]](https://seolalen.vn/wp-content/uploads/2022/09/de-thi-hoc-ky-2-lop-11-mon-toan-120x86.jpg)